I have been looking at aggregate home prices as if homes are a sort of inflation protected bond. Rent (or imputed rent) is what we spend to consume housing, as a service. Home ownership can (should) be seen as a financial security, where the cash flows are the perpetual rents on the property, less expenses. The sharp distinction between home ownership and housing consumption is widely dismissed, usually because ownership itself is seen as having value. This value means that most households who are able to own capture extensive surplus from ownership, so that price seems to be non-constraining. I'm afraid that this notion that housing prices aren't efficient is a significant factor feeding public distrust of housing markets and the idea that speculators can push prices up to inappropriate levels without triggering a selling response.
But, this is not that different from most other securities. There are some owners on the margin. And, in fact, in the aggregate, home prices appear to follow non-arbitrage price relationships with other fixed income securities over time. Home prices can be modeled by a simple fixed income model, such as this one:
Normally, the assumption is that house prices and rents will rise with general inflation levels, because higher rents will encourage new supply. This should be correct. The growth rate should be zero. And the fact that home prices have recently risen at a much higher rate than general inflation is taken as a sign of a "bubble". Strangely, as I have pointed out, vocal proponents of the "bubble" narrative have ignored the fact that there has been persistently high rent inflation, mostly coming from regulatory constraints in our major cities. The bust has been taken as an inevitable result of the effect of new supply on rent. But, the continuation of rent inflation, especially in our major cities, undercuts that explanation. In fact, there never was a strong supply response, and there is no strong supply response coming in the problem cities. The "bubble" was actually from a supply bust and the bust was from a demand bust that we created because we wrongly interpreted our supply problem as a demand problem.
This is why the Price/Rent ratio rose more using the Case-Shiller 10 City index (which includes the cities with the worst supply constraints) than it did in the national index. And the Case-Shiller National Index rose higher than a measure using rent income and home values from the BEA and the Federal Reserve. I think this is because the higher Price/Rent ratios in the major cities is a product of the persistent rent inflation (a growth rate in our equation above) which is due to regulatory supply constraints. The only places we can build are the places with lower Price/Rent ratios. Case-Shiller tracks the values of individual homes very well, but since marginal new homes must be homes with lower prices, Case-Shiller is a biased measure of the value of the home of the typical household.
 So, there might be a growth rate informing home prices, and that growth rate would be the expected rate of rent inflation. Here is a more detailed version of our valuation model, in nominal terms. As a first step, here, I am using the rate on 30 year mortgages as a proxy for the discount rate. It includes the real rate, the inflation expectation, and the real estate risk premium. Here I am using CPI shelter inflation as a proxy for the growth rate, which we can think of as representing general inflation plus expected rent inflation in excess of that. BEA table 7.12 gives us a measure of rent on all owner-occupied real estate, after expenses, and the Federal Reserve's Financial Accounts of the US gives us a measure of the total value of all owner-occupied real estate, which I use as a proxy for Home Price.
So, there might be a growth rate informing home prices, and that growth rate would be the expected rate of rent inflation. Here is a more detailed version of our valuation model, in nominal terms. As a first step, here, I am using the rate on 30 year mortgages as a proxy for the discount rate. It includes the real rate, the inflation expectation, and the real estate risk premium. Here I am using CPI shelter inflation as a proxy for the growth rate, which we can think of as representing general inflation plus expected rent inflation in excess of that. BEA table 7.12 gives us a measure of rent on all owner-occupied real estate, after expenses, and the Federal Reserve's Financial Accounts of the US gives us a measure of the total value of all owner-occupied real estate, which I use as a proxy for Home Price.We can solve the equation above for the growth rate by using our measures of net rent, home prices, and discount rate. We can call that the aggregate expected rate of forward rent inflation at any point in time. Then we can compare that to actual shelter inflation to see how closely expectations adhere to experience.
The problem is that the mortgage rate itself is a position on future inflation. In the 1970s, this was the dominant factor. So, mostly what we see here is that homeowners with a fixed rate mortgage saw sharp gains from 1975 to 1980, then saw sharp losses from 1981 to 1990. But, these gains and losses were largely a product of their short mortgage position in nominal terms. If we look at the later period where inflation was relatively stable, we see that the expected growth rate of rent cash flows is fairly stable, and follows the actual rate of rent cash flow growth pretty closely. There was not a sudden period in the 2000s where home buyers were depending on 5% or 10% rent growth. This is true even if we use Case-Shiller or FHFA home price indexes as our home price proxies.
Fortunately, for this analysis, our current supply problems seem to date to the mid 1990s, and we have some market measures of real discount rates that we can use for this period, so we can cancel out the expected general inflation measures in our denominator, and use a real valuation measure which is more fitting for a real asset like a house.
This is going to get long, and I'm going to dump a lot of graphs here, so the rest is below the fold.
***ADDED NOTE: I found better data to estimate city Price/Rent ratios with in the next post. So, some of the analysis below remains true, but the better data gives a slightly sharper result.
Now, the aggregate US price and rent measures will remain the same. But, I am going to repeat this analysis for the 15 cities which have both CPI owner-equivalent rent data and Case-Shiller home price data going back to at least 1995. In 1995, rent inflation had not been excessive nationally, or in the large cities, for about a decade, and home prices by both measures were at a low point. With the BEA & Fed data, I can actually create a measure for Price/Rent or its inverse, the implied yield. Since Case-Shiller and CPI data are indexes, I can't use them by themselves to create an implied yield. So, I have used 1995 as a baseline year, and assigned all cities the same Price/Rent and implied yield in that year as the national aggregate value. Estimates for Price/Rent and implied yield for each city are estimated from the changes over time after 1995.
For our denominator, for the risk free rate, we can use TIPS bonds to construct a 30 year real rate back to 1998. Real rates appear to have been fairly stable in the mid-1990s, so I have extended the real rate in 1998 back to 1995 in order to use the 1995 benchmark. For the risk premium, I have used the difference between the 30 year fixed rate mortgage and the 20 year treasury bond. Together, the 30 Year TIPS rate + the mortgage spread = the real discount rate for homes. Remember, that the mortgage is used here as a proxy for a real estate risk premium. Debt financing has nothing to do with this analysis. The point of this is to find the intrinsic value of unlevered homes.
 The expected growth rate is the rate of rent inflation minus the level of general CPI inflation. The "growth rate" I use is the difference between a city's Owner-Equivalent Rent inflation and national CPI core inflation. The TIPS bond rate used for the discount rate is adjusted with general CPI inflation, but over time general and core CPI inflation have not deviated from one another, and using core inflation here cuts down on period-to-period noise, so I have excused myself the slight disconnection.
The expected growth rate is the rate of rent inflation minus the level of general CPI inflation. The "growth rate" I use is the difference between a city's Owner-Equivalent Rent inflation and national CPI core inflation. The TIPS bond rate used for the discount rate is adjusted with general CPI inflation, but over time general and core CPI inflation have not deviated from one another, and using core inflation here cuts down on period-to-period noise, so I have excused myself the slight disconnection. There are 8 Case-Shiller 10 cities with data that I can use for this period, and 7 of the other Case-Shiller 20 cities. In addition, I have the aggregate US measures here, and also an estimate of the measures for the US outside of the Case-Shiller 10 cities - referred to in the graphs as US (x C-S 8). First, we see that the Price/Rent measures moved much higher than average in most of the Case-Shiller 10 cities. Among the Case-Shiller 20 cities, Seattle and Portland Price/Rent levels have moved up, but the other cities have Price/Rent levels similar to the aggregate national level. (Keep in mind, this is based on net rent in order to give us an estimate for net yield, so the P/R level here is higher than one constructed from gross rent.)
There are 8 Case-Shiller 10 cities with data that I can use for this period, and 7 of the other Case-Shiller 20 cities. In addition, I have the aggregate US measures here, and also an estimate of the measures for the US outside of the Case-Shiller 10 cities - referred to in the graphs as US (x C-S 8). First, we see that the Price/Rent measures moved much higher than average in most of the Case-Shiller 10 cities. Among the Case-Shiller 20 cities, Seattle and Portland Price/Rent levels have moved up, but the other cities have Price/Rent levels similar to the aggregate national level. (Keep in mind, this is based on net rent in order to give us an estimate for net yield, so the P/R level here is higher than one constructed from gross rent.) Now, if we flip this, we get Net Rent/Price, which is equal to the denominator in our valuation equation (Discount rate minus expected growth). The implied yield on most of the Case-Shiller 10 cities has moved much lower than the national number. And, for the Case-Shiller 20 cities, Portland and Seattle have lower yields while the other cities have yields similar to the national average.
Now, if we flip this, we get Net Rent/Price, which is equal to the denominator in our valuation equation (Discount rate minus expected growth). The implied yield on most of the Case-Shiller 10 cities has moved much lower than the national number. And, for the Case-Shiller 20 cities, Portland and Seattle have lower yields while the other cities have yields similar to the national average.Now, since we have an estimated discount rate for housing (the 30 year TIPS rate plus the mortgage spread), we can use that to determine what the expected excess growth rate of rent is in each of these cities. In other words, how much would rents need to rise (in excess of CPI inflation) over time in order to make the risk-adjusted returns to home ownership equal to the returns on 30 year TIPS bonds.
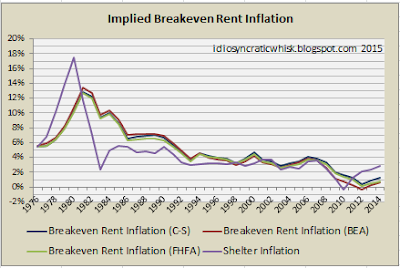
 This next graph shows the national aggregate rent inflation breakeven level that is implied by home prices and also the estimated breakeven level for the US outside of the Case-Shiller 10 cities.
This next graph shows the national aggregate rent inflation breakeven level that is implied by home prices and also the estimated breakeven level for the US outside of the Case-Shiller 10 cities.There are several things to note here. First, there is persistent rent inflation nationally, especially in the Case-Shiller 10 cities. Second, while we could quibble about the exact size of the risk premium that should be applied to the yield on home ownership, it is unlikely to be much higher than what I have used, and could be lower, since the mortgage spread includes prepayment risk. In terms of rent cash flows, there is no period where home prices depended on outrageous assumptions of cash flows. Prices were never far from reasonable DCF values. Third, since the crisis, prices have collapsed while rent inflation has returned sharply. Home prices now imply perpetual rent deflation. The one period where prices have clearly been out of equilibrium has been from 2009 to the present. Fourth, we can see from the difference in rent inflation between the two measures that much of the national rise in housing costs before the crisis came from the supply constraint in the cities. But, since the crisis, rent inflation has been the same within and outside of the Case-Shiller 10 cities, because the supply constraint since then has been from the collapsed mortgage market, which has had a nationwide effect. Fifth, on a national scale, supply finally was beginning to expand enough to eliminate excess rent inflation. But, home prices at the time did not reflect any expectation of future rent inflation. By this measure, in the period leading up to the crisis, the most conservative home prices were the prices in 2003 and 2004, near the top of the boom! That is because this breakeven growth rate is effected 1:1 by long term real interest rates. Since home prices are sticky, both up and down, they don't move in real time as quickly as bond yields when long term yields are volatile. (Keep in mind these are 30 year real yields, which are not directly under Fed control. It would not be accurate to say that low 30 year real yields are the product of monetary accommodation. But, even conceding that, what this shows is that cash wasn't particularly flowing into housing. From 2000 to 2004, home prices were lagging long term real bond prices.)
Below, I will include the Breakeven Rent Inflation graph for each city. Rent inflation tends to be much more noisy in the city-specific measures because local conditions create a lot of volatility in the short term. But, I think readers will see that the cities with the most home price appreciation have implied rent inflation expectations well within the range of persistent excess rent inflation. Portland is the only exception to that. Interestingly, the cities where implied rent expectations are higher than experienced rent inflation are generally cities where nominal home prices have not been unusually high, but rent inflation has been low or negative - Detroit, Cleveland, etc.
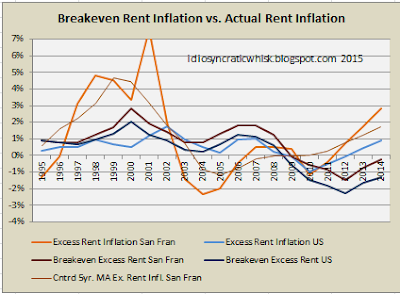
 Here are two scatterplots comparing each city's average excess rent inflation to its average implied rent inflation expectations - first for the period 1995-2007, then for the entire 1995-2014 period. I have colored the Detroit and Cleveland points purple. I have colored the Chicago, New York City, Los Angeles, and San Francisco points light blue. These are the four largest metro areas, representing about 20% of US residential real estate, by value. Except for Chicago, they seem to be the source for much of the statistical trends of higher income inequality and rising housing costs. In the 1995-2007 period, these cities line up right along the 45 degree angle line. In other words, during the boom period, the relative change in home prices in these cities correlated very strongly with the persistent trend in rising rents. The national numbers, shown both in the aggregate and for the US outside of the Case-Shiller 10 cities (the lower of the two black dots in each graph) are slightly above the 45 degree line for the boom period, but, as mentioned above, this appears to come mostly from low rents in stagnant or declining cities. And there is the same counterintuitive pattern regarding time. Home prices appear to have implied higher growth expectations in the late 1990s when nominal prices were low, and later when nominal prices were higher, expected rent growth was below actual rent inflation.
Here are two scatterplots comparing each city's average excess rent inflation to its average implied rent inflation expectations - first for the period 1995-2007, then for the entire 1995-2014 period. I have colored the Detroit and Cleveland points purple. I have colored the Chicago, New York City, Los Angeles, and San Francisco points light blue. These are the four largest metro areas, representing about 20% of US residential real estate, by value. Except for Chicago, they seem to be the source for much of the statistical trends of higher income inequality and rising housing costs. In the 1995-2007 period, these cities line up right along the 45 degree angle line. In other words, during the boom period, the relative change in home prices in these cities correlated very strongly with the persistent trend in rising rents. The national numbers, shown both in the aggregate and for the US outside of the Case-Shiller 10 cities (the lower of the two black dots in each graph) are slightly above the 45 degree line for the boom period, but, as mentioned above, this appears to come mostly from low rents in stagnant or declining cities. And there is the same counterintuitive pattern regarding time. Home prices appear to have implied higher growth expectations in the late 1990s when nominal prices were low, and later when nominal prices were higher, expected rent growth was below actual rent inflation. Almost all of the cities move below the 45 degree line when we include the full period, because home prices since the crisis have been very low with regard to long term real interest rates since so many households are unable to access housing credit markets.
Almost all of the cities move below the 45 degree line when we include the full period, because home prices since the crisis have been very low with regard to long term real interest rates since so many households are unable to access housing credit markets. Regarding the period ending in 2007, it looks like rent inflation expectations in those problem metro areas are expected to persist. In the other cities, most of the persistent rent inflation gets imbedded in home prices through growth expectations, but not all. This makes sense, as those rising rents come with political risk, so homebuyers are capturing some alpha in places where there has been some rent inflation, but where opponents to housing expansion aren't as ensconced.
Regarding the period ending in 2007, it looks like rent inflation expectations in those problem metro areas are expected to persist. In the other cities, most of the persistent rent inflation gets imbedded in home prices through growth expectations, but not all. This makes sense, as those rising rents come with political risk, so homebuyers are capturing some alpha in places where there has been some rent inflation, but where opponents to housing expansion aren't as ensconced. Keeping in mind that the outliers in the 1995-2007 plot are the smaller markets, so the relationship between experienced rent and expected rent is stronger than the basic unweighted scatterplot suggests, a regression line on this relationship still would appear to have a y-intercept above zero of up to about 0.5%. This could be because I have overestimated the real estate risk premium. Or, it could represent nationwide positive price pressures coming from credit expansion, demand released due to low nominal interest rates, tax benefits, or speculation. It would also reflect the disconnect we see between home prices and rents in economically failing cities with falling housing demand.
Keeping in mind that the outliers in the 1995-2007 plot are the smaller markets, so the relationship between experienced rent and expected rent is stronger than the basic unweighted scatterplot suggests, a regression line on this relationship still would appear to have a y-intercept above zero of up to about 0.5%. This could be because I have overestimated the real estate risk premium. Or, it could represent nationwide positive price pressures coming from credit expansion, demand released due to low nominal interest rates, tax benefits, or speculation. It would also reflect the disconnect we see between home prices and rents in economically failing cities with falling housing demand.
 Nationally, home prices rose by about 125% during this period. I roughly divide that increase into thirds - each creating about a 30% gain. One third of the rise is due to lower real interest rates. (Not because of mortgage rates, but because it increases the present value of future rent cash flows, and therefore the intrinsic value of the home.) One third of the rise is due simply to rising rents over time. Homes with 30% higher rents should be expected to have 30% higher prices. And, one third is the effect of this changing growth factor. As measured, this could be explained by either realistic persistent rent growth (the supply problem) or by unrealistic expectations or factors that push price/rent ratios above previously typical levels (credit, demand, tax benefits, speculation, sticky prices in declining markets). So, there is some room for demand-based factors in the rising home prices of the 2000s, but those factors appear to amount to less than 10%-15% of the 125% national price appreciation.
Nationally, home prices rose by about 125% during this period. I roughly divide that increase into thirds - each creating about a 30% gain. One third of the rise is due to lower real interest rates. (Not because of mortgage rates, but because it increases the present value of future rent cash flows, and therefore the intrinsic value of the home.) One third of the rise is due simply to rising rents over time. Homes with 30% higher rents should be expected to have 30% higher prices. And, one third is the effect of this changing growth factor. As measured, this could be explained by either realistic persistent rent growth (the supply problem) or by unrealistic expectations or factors that push price/rent ratios above previously typical levels (credit, demand, tax benefits, speculation, sticky prices in declining markets). So, there is some room for demand-based factors in the rising home prices of the 2000s, but those factors appear to amount to less than 10%-15% of the 125% national price appreciation. Added PS: One additional factor on the regression, which I didn't address above, is that the regression of the expected inflation between cities could be biased by my decision to peg Price/Rent levels in 1995. If high rent cities already had higher P/Rs in 1995, then my analysis is understating their P/Rs and overstating the current P/Rs of low cost cities. My data shorthand could be flattening the relationship between rent inflation and expected rent inflation. I'm looking at some data that might help fix this problem.
Added PS: One additional factor on the regression, which I didn't address above, is that the regression of the expected inflation between cities could be biased by my decision to peg Price/Rent levels in 1995. If high rent cities already had higher P/Rs in 1995, then my analysis is understating their P/Rs and overstating the current P/Rs of low cost cities. My data shorthand could be flattening the relationship between rent inflation and expected rent inflation. I'm looking at some data that might help fix this problem.











No comments:
Post a Comment